 |
第9回(2002.10.03) デシジョンツリー |
||||||
| 今回は、プロジェクトにおける決定分析に用いられる手法としてデシジョンツリーを解説する。決定分析そのものは、プロジェクトマネジメントではあらゆる場面で出てくる。もっとも重要な場面はリスクマネジメントである。 ◆デシジョンツリーとは デシジョンツリーは、期待値の算出をあらわす図で、 ・決定ノード ・機会事象ノード ・終端ノード を結んだグラフである。 (1)決定ノード 決定ノードは意思決定者がコントロールできる変数や行動。図のように□で表す 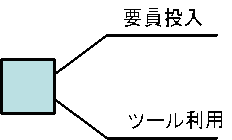 2)機会事象ノード 機会事象ノードは意思決定者がコントロールできない変数や行動で、図のように○で表す 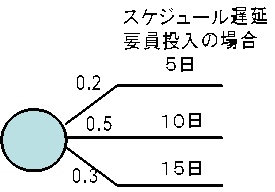 (3)終端ノード 結果価値を得る最終点で、開いたリンクで表す 基本的にはこの3つのノードからなるグラフであるが、これに3種類のラベルをつけることになっている。 一つは機会事象ノードからそれぞれのリンクに進む確率。二つ目はノードの期待値。これはデシジョンツリーを解いてしていく段階で計算される。三つ目は結果価値。これは本来のキャッシュフローに対して割引された現在価値になる。 ◆デシジョンツリーの計算 デシジョンツリーの計算はそんなに難しくはない。以下の3つのルールを守りながら終端ノードから逆算していく。 ・決定ノードでは最適な代替案と置き換える ・機会事象ノードでは、確率と枝の価値から期待値を算出する。これがノードとそのリンクになる ・費用価値がある場合には、右から左に移すときにその値を差し引く ◆例題 計画期間を7日間残して、ソフトウエア開発タスクが遅れ気味のときに、その対策として2つの方法を考える。一つは要員投入であり、もう一つがツールの利用である。ただし、簡単のためにツールは直ぐに投入でき、すべての人が直ぐに使いこなせるものとする。以下に状況設定を示す。 まず、遅延であるが、 <要員投入の場合:遅延1日につき10万円> 遅延日数 確率 コスト 10日 0.2 100万円 5日 0.7 50万円 1日 0.1 10万円 <開発ツールの利用の場合;遅延1日につき5万円> 遅延日数 確率 コスト 3日 0.1 15万円 2日 0.3 10万円 1日 0.6 5万円 と予想される。このタスクがクリティカルパス上にあるかどうかは確率的な問題になるので、それぞれ、クリティカルパス上にある確率を 要員投入の場合 ツール利用の場合 0.2 とする。また、計画期間内の追加費用は 要員投入の場合 70万円 ツール利用の場合 レンタル料 90万円 とする。このとき、上のルールに従い、デシジョンツリーの計算を行う。各ノードの計算をすると EVM(4)=0.2×100+0.7×50+0.1×10=56 EVM(5)=0.1×15+0.3×10+0.6×5=7.5 EVM(2)=0.4×56+0.6×0=22.4 EVM(3)=0.2×7.5+0.8×0=1.5 EVM(1)=最大 22.4+70=92.4 =最小 1.5+90=91.5 となるので、デシジョンツリーを書いてみると図のようになる。 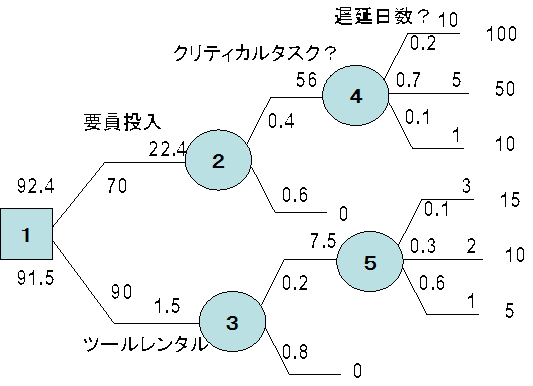 結果として費用の期待値は 要員投入の場合 92.4万円 ツール利用の場合 91.5万円 でツール利用の方が期待金銭価値が小さく、このケースの期待金銭価値はすべて費用であるので、ツール利用を選ぶのが合理的であることが分かる。 ◆デシジョンツリーの使い方 上の例はプロジェクトの中の意思決定の例としては、そんなに複雑なものではない。しかし、この例でも直感的に判断することは結構難しいだろう。そのような場合に、客観性のある判断をできることにデシジョンツリーの利用価値がある。 |
|||||||
| 参考文献: John Schuyler「Risk and Decision Analysis in Projects」,PMI(2001) |
|||||||
| スポンサードリンク | |||||||
| 読者からのコメント | |||||||
|
|||||||
■本稿に対するご意見,ご感想をお聞かせください.■ ■は必須入力です |
|||||||
| このコンテンツは「プロジェクトマネージャー養成マガジン」としてメルマガで配信されています.メルマガの登録はこちらからできます. | |||||||